unity-priestsAndDevils-V3

priestsAndDevils-V3

基于当前游戏状态，给出正确解路径下一步提示。

• priestsAndDevils-V3
  • 游戏状态图
    • 分析
      • 游戏状态定义
      • 游戏状态变换
      • 正确解路径
    • cpp code
    • cpp To csharp
  • 游戏改进
    • 预览图
    • 视频

游戏状态图

分析

我们的目标：输入当前游戏状态，查找正确解路径，并返回对应的下一游戏状态。

所以我们需要 定义游戏状态，定义状态如何转换和选择算法。

游戏状态定义

对于牧师与魔鬼游戏，我们首先需要给定我们对于游戏状态的定义。对于游戏状态，我采用如下定义：
一个游戏状态由所有游戏对象的位置决定。即所有游戏对象的位置的集合构成一个游戏状态。
可能不好理解，举例说明一下。初始的游戏状态为：左岸无牧师，无魔鬼，右岸三牧师，三魔鬼，船在右岸；获胜游戏状态为：左岸三牧师，三魔鬼，右岸无牧师，无魔鬼，船在左岸。对于每个状态，我们需要 判断其合法性，即游戏状态是否会结束游戏。因此，可以将游戏状态提取为下面的数据结构：

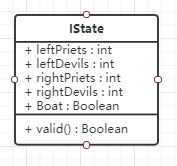
四个整数存储两岸的游戏对象数量，最后一个布尔型变量 Boat 代表船的位置，true 在左岸，false 在右岸，vaild 操作可以判断当前游戏状态是否合法。

游戏状态变换

定义完游戏状态，我们考虑下一件事，状态与状态之间如何进行变动。我们的游戏是通过 游戏对象的移动，改变游戏状态，即人物搭船移动到对岸，游戏状态改变。那么我们的状态变动就可以从两大类人物动作中得到：单人过河和双人过河。

船只的位置也影响游戏状态，且它的位置影响下一游戏状态的两岸人物数量变动，所以综合考量后可得出一个状态向下一个状态的所有动作行为：

• 船在左岸
  • 单人过河
    • 牧师过河
    • 魔鬼过河
  • 双人过河
    • 牧师 + 牧师过河
    • 牧师 + 魔鬼过河
    • 魔鬼 + 魔鬼过河
• 船在右岸
  • 单人过河
    • 牧师过河
    • 魔鬼过河
  • 双人过河
    • 牧师 + 牧师过河
    • 牧师 + 魔鬼过河
    • 魔鬼 + 魔鬼过河

这个是我们实现推测正确解路径的关键。

正确解路径

我们现在的工作就是，如何从最左边的当前状态，获得下一状态，然后不断进行，找到结束状态，得到正确解路径。这个图就像是树一样，所以有两种策略可以完成这个工作：DFS 和 BFS。

在这里，我采用 BFS，因为最短求解路径是我想要的。大家也可以试试写一下 DFS。

算法描述：

1. 当前状态入队
2. 队列不为空：
   • 取队头状态
   • 访问状态节点：
     • 结束状态?
       • 是：输出
       • 否：计算下一状态，合法状态入队

cpp code

首先，用熟悉的 c++ 实现一遍(当时正好只有 dev，所以就先写了 c++ 版本)。

注意体会状态合法的条件判断(这里一开始写错了，但没有注意，结果在算法中 Debug)。

其他重载是为了队列操作需要，可以顺便回顾 c++。

class IState {
public:
  int leftPriests;
  int leftDevils;
  int rightPriests;
  int rightDevils;
  bool boat;
  IState* parent;

  IState();

  IState(int leftPriests, int leftDevils, int rightPriests,
    int rightDevils, bool boat, IState* parent);

  IState(const IState &another);

  IState& operator = (IState another);

  bool operator == (const IState &another) const;

  bool operator != (const IState &another) const;

  bool valid() {
    return ((leftPriests == 0 || leftPriests >= leftDevils) &&
      (rightPriests == 0 || rightPriests >= rightDevils));
  }
};

在实现 BFS 时，我们加入一个 visited 队列，对搜索进行优化，避免出现死循环，因为在这个游戏中，可以在两个状态间循环操作；合法状态入队也减少了搜索量，虽然这在游戏中会直接结束游戏，但对于算法而言，是一种剪枝优化。

IState bfs(IState &start, IState &end) {
  queue<IState> found;
  vector<IState> visited;
  IState temp;
  found.push(start);

  while (!found.empty()) {
    temp = found.front();

    // Get Answer
    if (temp == end) {
      while(*(temp.parent) != start) {
        temp = *(temp.parent);
      }
      return temp;
    }

    found.pop();
    visited.push_back(temp);

    IState next = temp;
    next.parent = new IState(temp);
    temp.parent = next.parent;
    // next node
    if (next.boat) {
      next.boat = !next.boat;
      // one move to right
      if (next.leftPriests > 0) {
        next.leftPriests--;
        next.rightPriests++;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
      next = temp;
      next.boat = !next.boat;
      if (next.leftDevils > 0) {
        next.leftDevils--;
        next.rightDevils++;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
      // two moves to right
      next = temp;
      next.boat = !next.boat;
      if (next.leftDevils > 0 && next.leftDevils > 0) {
        next.leftPriests--;
        next.leftDevils--;
        next.rightPriests++;
        next.rightDevils++;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
      next = temp;
      next.boat = !next.boat;
      if (next.leftDevils > 1) {
        next.leftDevils -= 2;
        next.rightDevils += 2;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
      next = temp;
      next.boat = !next.boat;
      if (next.leftPriests > 1) {
        next.leftPriests -= 2;
        next.rightPriests += 2;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
    } else {
      next.boat = true;
      // one move to left
      if (next.rightPriests > 0) {
        next.rightPriests--;
        next.leftPriests++;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
      next = temp;
      next.boat = !next.boat;
      if (next.rightDevils > 0) {
        next.rightDevils--;
        next.leftDevils++;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
      // two moves to left
      next = temp;
      next.boat = !next.boat;
      if (next.rightDevils > 0 && next.rightDevils > 0) {
        next.rightPriests--;
        next.rightDevils--;
        next.leftPriests++;
        next.leftDevils++;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }

      }
      next = temp;
      next.boat = !next.boat;
      if (next.rightDevils > 1) {
        next.rightDevils -= 2;
        next.leftDevils += 2;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
      next = temp;
      next.boat = !next.boat;
      if (next.rightPriests > 1) {
        next.rightPriests -= 2;
        next.leftPriests += 2;
        if (next.valid() &&
          find(visited.begin(), visited.end(), next) == visited.end()) {
          found.push(next);
        }
      }
    }
  }
}

cpp To csharp

我们将所有代码封装在 IState 类中。其中，有以下几点需要注意：

1. C# 对象本身就是引用传值，所以 c++ 的指针可以直接转变成类对象本身。
   • 时刻注意 C# 的赋值语句，类对象赋值为引用赋值。
2. C# 运算符重载 和 C# 中 Equals 和 == 运算符)
   • C# 可以重载操作符，但需要成对重载
   • C# 判断相等默认调用 Equals 方法
   • C# 重写 Equals 方法，必须同时重写 GetHashCode 方法

基本的重复代码略去展示，C# 的代码如下:

public class IState {
    public int leftPriests;
    public int leftDevils;
    public int rightPriests;
    public int rightDevils;
    public bool boat;
    public IState parent;

    public IState();

    public IState(int leftPriests, int leftDevils, int rightPriests,
      int rightDevils, bool boat, IState parent);

    public IState(IState another);


    public static bool operator ==(IState lhs, IState rhs);

    public static bool operator !=(IState lhs, IState rhs);

    public override bool Equals(object obj) {
      if (obj == null) {
        return false;
      }
      if (obj.GetType().Equals(this.GetType()) == false) {
        return false;
      }
      IState temp = null;
      temp = (IState)obj;
      return this.leftPriests.Equals(temp.leftPriests) &&
        this.leftDevils.Equals(temp.leftDevils) &&
        this.rightDevils.Equals(temp.rightDevils) &&
        this.rightPriests.Equals(temp.rightPriests) &&
        this.boat.Equals(temp.boat);
    }

    public override int GetHashCode() {
      return this.leftDevils.GetHashCode() + this.leftPriests.GetHashCode() +
        this.rightDevils.GetHashCode() + this.rightPriests.GetHashCode() +
        this.boat.GetHashCode();
    }

    public bool valid();

    public static IState bfs(IState start, IState end) {
      Queue<IState> found = new Queue<IState>();
      Queue<IState> visited = new Queue<IState>();
      IState temp = new IState(start.leftPriests, start.leftDevils,
        start.rightPriests, start.rightDevils, start.boat, null);
      found.Enqueue(temp);

      while (found.Count > 0) {
        temp = found.Peek();

        if (temp == end) {
          while (temp.parent != start) {
            temp = temp.parent;
          }
          return temp;
        }

        found.Dequeue();
        visited.Enqueue(temp);

        // next node
        if (temp.boat) {
          // one move to right
          if (temp.leftPriests > 0) {
            IState next = new IState(temp);
            next.parent = new IState(temp);
            next.boat = false;
            next.leftPriests--;
            next.rightPriests++;
            if (next.valid() && !visited.Contains(next) && !found.Contains(next)) {
              found.Enqueue(next);
            }
          }
          if (temp.leftDevils > 0) { /* ... */}
          // two moves to right
          if (temp.leftDevils > 0 && temp.leftDevils > 0) {/* similar to before code */}
          if (temp.leftDevils > 1) { /* ... */}
          if (temp.leftPriests > 1) { /* ... */}
        } else {
          //one move to left
          if (temp.rightPriests > 0) { /* ... */}
          if (temp.rightDevils > 0) { /* ... */}
          //two moves to left
          if (temp.rightDevils > 0 && temp.rightDevils > 0) { /* ... */}
          if (temp.rightDevils > 1) { /* ... */}
          if (temp.rightPriests > 1) { /* ... */}
        }
      }
      return null;
    }
  }

游戏改进

1. 角色颜色区分：绿色牧师，红色魔鬼，棕色船只
2. 根据当前状态给出最短正确路径的下一状态
   交由代码运算，而非直接根据手写状态图进行简单的 if-else 给出

优点：游戏状态增加时，只需更改状态变化的逻辑代码，而不必重写状态图

游戏变动：

1. 在 Model 文件夹内完成 IState 类
2. 在 View 文件夹的 UI 类页面中加入一个 button 和一个 label，并在 OnGUI 函数中绑定点击事件：
   • 根据当前状态得到下一步状态
   • 根据下一步状态，刷新 label 的显示字符串。

预览图

视频

Video