Fork me on GitHub

Leetcode-TEN-wordBreak

发表于 | 分类于 | 阅读次数:

Word Break Problems

Word Break

Description

Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.

Note:

The same word in the dictionary may be reused multiple times in the segmentation.
You may assume the dictionary does not contain duplicate words.

Example

  1. Example One:

    Input: s = “leetcode”, wordDict = [“leet”, “code”]
    Output: true
    Explanation: Return true because “leetcode” can be segmented as “leet code”.

  2. Example Two:

    Input: s = “applepenapple”, wordDict = [“apple”, “pen”]
    Output: true
    Explanation: Return true because “applepenapple” can be segmented as “apple pen apple”.
    Note that you are allowed to reuse a dictionary word.

  3. Example Three:

    Input: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
    Output: false

Analysis

题目意思为，给出一个字符串，和一个包含某些字符串的字典，判断给出字符串能否分割为字典内的字符串序列。如样例一，leetcode 和字典[“leet”, “code”]，这是可行的，因为 leetcode 可以分割为 “leet code”。

我们来试试 dp (虽然这个 dp 和普通循环的算法差别不是特别大，希望看看其他大佬的想法)。
设输入字符串为 $str[0…n-1]$，字典为 $dict=[…]$。构造 $dp[0…n]$，其中 $dp[m], m \in [0, n]$ 表示 $str[0…m]$ 能否被分割为合法的字典串序列。
原问题的解答就是 $dp[n]$。对于子问题：$dp[i]$ 的值，我们考量所有串 $str[j, i], j \in [0, i-1]$，当 $dp[j]$ 不合法时，那么无论串 $str[j, i]$ 是否合法，$dp[i]$ 都不合法；当 $dp[j]$ 合法时，那么 $dp[i]$ 合法性取决于串 $str[j, i]$ 的合法性。但是，对于 $dp[i]$ 的最终取值，它是所有 $j$ 决定的 $dp[i]$ 的值的或。可以考虑这个情况:
str = abcd，dict = [“a”, “bcd”]，dp[0…4] = {true, true, false, false, unknown}。
当前正在判断 $dp[4]$，当 $j = 3$ 时，计算得 $dp[4] = false$($dp[3] = fasle$)，但是，可以看到，继续计算到 $j = 1$ 时，计算得 $dp[4] = true$($dp[1] = true$ 且串 bcd 合法)，所以 $dp[4]$ 的值是所有求得的 $dp[4]$ 值的或。
对于 $dp[0]$，我们设为 true，因为空串属于字典是可以定义的。

下面是计算式：
$$dp[i] = \bigvee\limits_{0 <= j < i} (dp[j] \land valid(substr(j, i - j)))$$

根据计算式子，我们写出伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
dp[0...n] = false
dp[0] = true
for i in [1 : n]:
  for j in [i-1 : 0]:
    # unnecessary to compute when dp[j] = false in OR computation
    if (dp[j]):
      if (valid(substr(j, i-j))):
        dp[i] = true
        # Valid break to next position because 
        # the number of solutions is not important
        break

return dp[n]

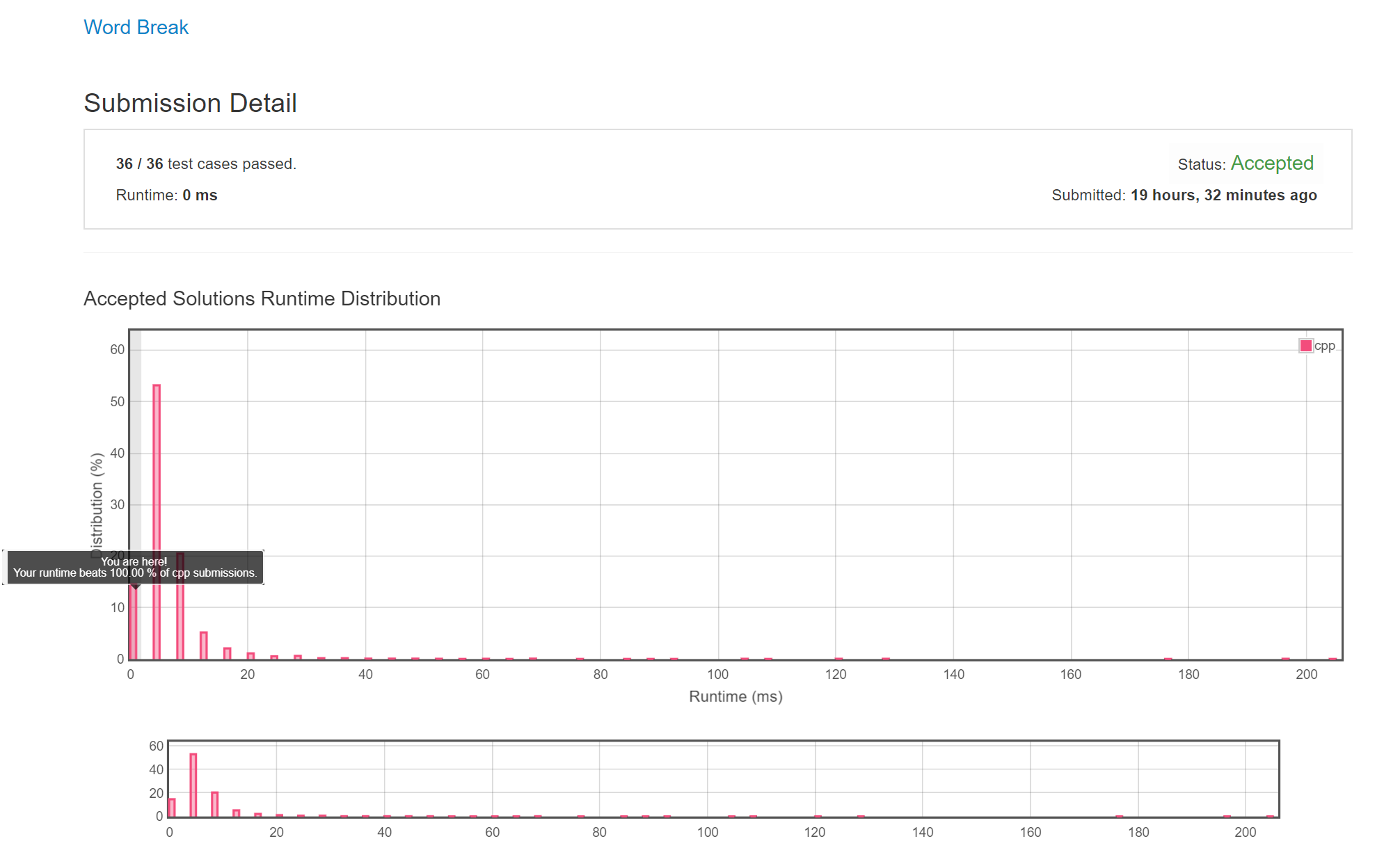
AC Picture

AC

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool wordBreak(string s, vector<string> &dict) {
  int size = s.size();
  vector<bool> dp(size + 1, false);
  dp[0] = true;
  
  for (int i = 1; i <= size; ++i) {
    for (int j = i - 1; j >= 0; --j) {
      if (dp[j]) { // unnecessary to compute when dp[j] = false in OR computation
        string word = s.substr(j, i - j);
        if (find(dict.begin(), dict.end(), word) != dict.end()) {
          dp[i] = true;
          // Valid break to next position because 
          // the number of solutions is not important
          break;
        }
      }
    }
  }
  
  return dp[size];
}

Word Break II

Description

Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences.

Note:

The same word in the dictionary may be reused multiple times in the segmentation.
You may assume the dictionary does not contain duplicate words.

Example

  1. Example One:

    Input:
    s = “catsanddog”
    wordDict = [“cat”, “cats”, “and”, “sand”, “dog”]
    Output:
    [
    “cats and dog”,
    “cat sand dog”
    ]

  2. Example Two:

    Input:
    s = “pineapplepenapple”
    wordDict = [“apple”, “pen”, “applepen”, “pine”, “pineapple”]
    Output:
    [
    “pine apple pen apple”,
    “pineapple pen apple”,
    “pine applepen apple”
    ]
    Explanation: Note that you are allowed to reuse a dictionary word.

  3. Example Three:

    Input:
    s = “catsandog”
    wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
    Output:
    []

Analysis

题目意思为输出给定串可分割的所有合法字典序列。我们可以利用上面的 dp 进行适当的改造，来构造答案：

  1. 增加一个二维数组，用于存储节点 i 的父节点；
  2. 当发现一个解时，存储其父节点值，并继续向前求解，而不是跳过；

算法伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
dp[0...n] = false
dp[0] = true
int graph[0...n][] # store the parent node
graph[0] = [-1]
for i in [1 : n]:
  for j in [i-1 : 0]:
    # unnecessary to compute when dp[j] = false in OR computation
    if (dp[j]):
      if (valid(substr(j, i-j))):
        dp[i] = true
        graph[i].push(j)

return dfs(graph, n)

最终，我们可以得到一个存储了当前有解节点的父节点的二维数组，通过样例二来说明：
输入: str = “pineapplepenapple”, dict = [“apple”, “pen”, “applepen”, “pine”, “pineapple”]
当 i = 4，j = 0，得到 pine，dp[4] = true，graph[4] = [0]；
当 i = 9，j = 5，得到 apple，dp[9] = true，graph[9] = [5]；
当 i = 9，j = 0，得到 pineapple，dp[9] = true，graph[9] = [5，0]；
当 i = 12，j = 9，得到 pen，dp[12] = true，graph[12] = [9]；
当 i = 12，j = 4，得到 applepen，dp[12] = true，graph[12] = [9，4]；
当 i = 17，j = 12，得到 apple，dp[17] = true，graph[17] = [12]；
最终，我们得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
dp[0...17] = {T,F,F,F,T,F,F,F,F,T,F,F,T,F,F,F,F,T}
graph[0...17] = [
  [-1],
  [],
  [],
  [],
  [0],
  [],
  [],
  [],
  [],
  [5,0],
  [],
  [],
  [9,4],
  [],
  [],
  [],
  [],
  [12]
]

根据 graph，我们利用 dfs 可以重构出所有的解序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
# dfs current node(int)
# the order of the child node is not matter
void dfs(int graph[][], int &node) {
  if (node <= 0) return;

  int size = graph[node].size();
  for (int i = 0; i < size; ++i) {
    dfs(graph, graph[node][i]);

    # Process
  }
  return;
}

我们根据需要，每次 dfs 返回一个字符串数组，然后处理返回的字符串数组。对于返回的字符串数组，代表其子节点对应的解序列个数，每一个解序列，我们需要加上当前节点的字符串(有解序列则添加一个空格)。最终构造出所有的解序列。

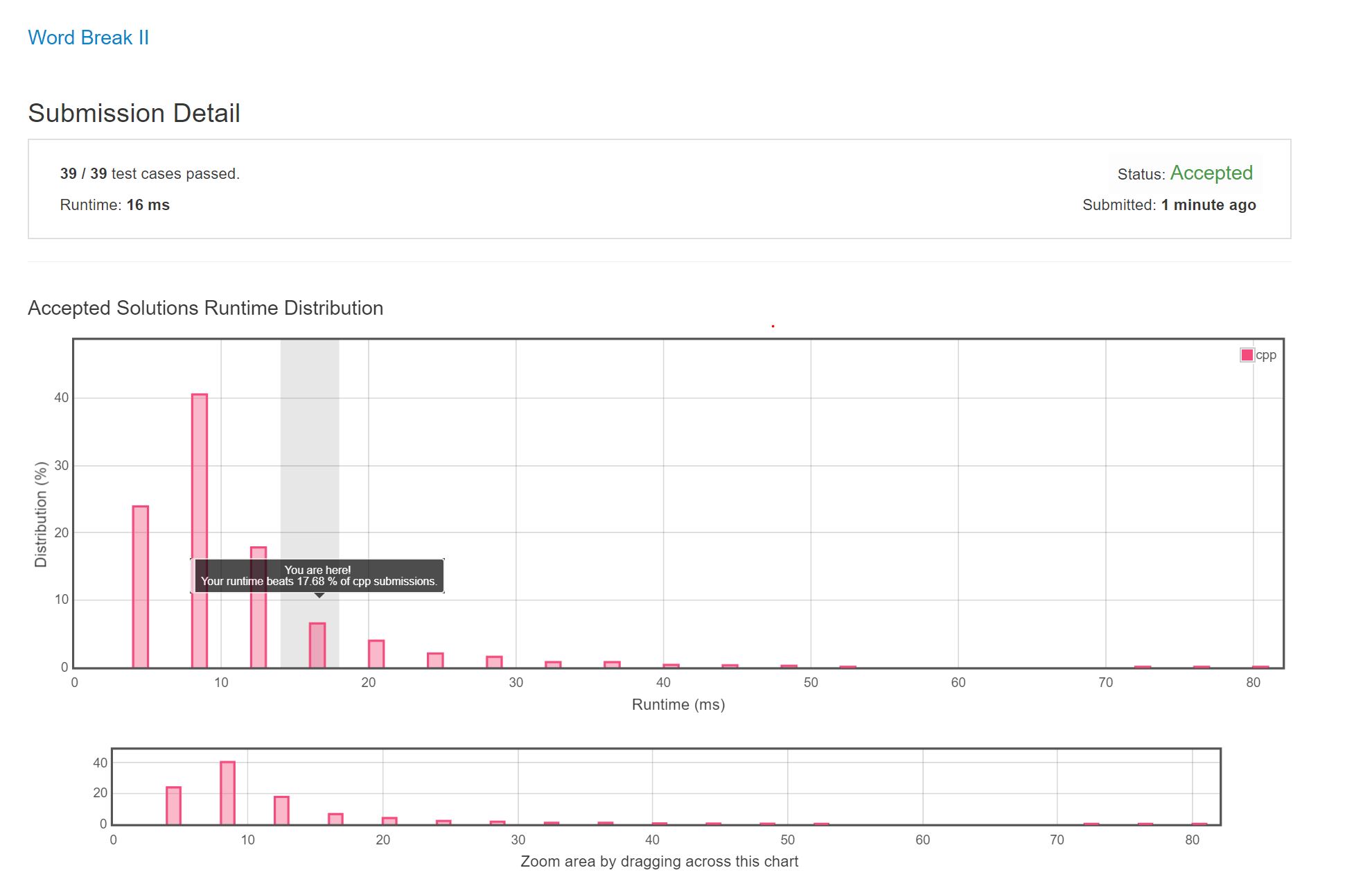
AC Picture

AC

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
vector<string> wordBreak(string &s, vector<string>& dict) {
  int size = s.size();
  
  vector<vector<int> > graph;
  graph.resize(size + 1);
  graph[0].push_back(-1);
  
  vector<bool> dp(size + 1, false);
  dp[0] = true;
  
  for (int i = 1; i <= size; ++i) {
    for (int j = i - 1; j >= 0; --j) {
      if (dp[j]) {
        string word = s.substr(j, i - j);
        if (find(dict.begin(), dict.end(), word) != dict.end()) {
          dp[i] = true;
          graph[i].push_back(j);
        }
      }
    }
  }
  
  return dfs(s, graph, size);
}

// DFS to construct the result
// End node as origin node
vector<string> dfs(string &s, vector<vector<int> > &graph, int &node) {
  vector<string> ans;
  if (node <= 0) {
    ans.push_back("");
    return ans;
  }

  int size = graph[node].size();
  for (int i = 0; i < size; ++i) {
  // cur node string
    string str = s.substr(graph[node][i], node-graph[node][i]);
    vector<string> sub = dfs(s, graph, graph[node][i]);

    // Process the child node string with cur node string
    int loop = sub.size();
    for (int j = 0; j < loop; ++j) {
      sub[j] += (sub[j] == "" ? "" : " ") + str;
      ans.push_back(sub[j]);
    }
  }
  return ans;
}