Fork me on GitHub

Leetcode-TWO-ReversePairs

发表于 | 分类于 | 阅读次数:

ReversePairs

Description

Question link

Given an array nums, we call (i, j) an important reverse pair if i < j and nums[i] > 2*nums[j].

You need to return the number of important reverse pairs in the given array.

Examples

Example1:
Input: [1,3,2,3,1]  
Output: 2

Example2:
Input: [2,4,3,5,1]  
Output: 3

Note:
The length of the given array will not exceed 50,000.
All the numbers in the input array are in the range of 32-bit integer.

Analysis & Code

题目大意为，在一个数组 array中，对于数组内的两个元素 ai 和 aj，如果 ai > 2 * aj 且 i < j，那么这样一个数对(i,j)称为 reverse pair。先给出数组，需要找出这样的数对个数。

General Solution

我们可以有一个大胆的想法，暴力 双重循环，然后发现 TL。所以老老实实的来分析一下。

Divide and Conquer Solution

我们可以这样考虑，对于给定的数组arr(0, len)，我们从中间分割为两个数组left(0, mid)和right(mid, len)

对于我们的问题 T(0, len)，我们就可以变为求解左半部分，求解右半部分，求解跨越左半部分和右半部分共三个求解过程，即：

T(0, len) = T(0, mid) + T(mid, len) + C

其中 C 为跨越左右两部分的问题。其实这个就是我们的子问题。因为，对于左右两部分，不断划分到最后，是单一元素，这时左右部分跨越就是最终的问题。

对于 C 这个子问题，我们去数数对就好了。数对的条件有两个：ai > 2 * aj 且 i < j。其中 i < j 是天然满足的，因为只要在右半部分找 j， 左半部分找 i，就可以了。需要判断的是条件: ai > 2 * aj。

但如果直接搜索，那么 C 的复杂度是 $O(n^2)$。运用 Master 定理，$T(n) = 2T(n/2) + O(n^2)$ 的复杂度依旧是 $O(n^2)$。这个算法并没有达到优化复杂的目的。

但是，我们可以发现，左半部分和右半部分数据的次序，对于我们来说，是无用的。如果我们的数据左右是有序的，我们就可以采用双指针游走的方法，来计算数对。

数组有序时，s采用 双指针 计算数对方法如下：一个指针指向左侧初始位置，一个指向右侧初始位置。如果满足 ai > 2 * aj，那么右侧指针向尾部移动。对于每一个 i，我们移动 j 后，不需重置 j，因为 i 是有序的，下一个 i 会比前一个大，那么与前一个 i 构成数对的 j，也可以与下一个 i 构成数对，所以 i 和 j 的单向移动，就可以算出这个子问题中的数对数量。

那么如何做到数组有序呢？我们在每次归并的时候，同时进行排序，就行了。

我们再来看看复杂度。子问题的双指针移动为 $O(n)$，排序调用 sort 最差为 $O(nlogn)$，所以子问题的事件复杂度为 $O(nlogn)$。最终的复杂度也就是 $O(nlogn)$，达到优化目的。

下面附上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int reversePairs(vector<int>& nums) {
    return subSolution(nums, 0, nums.size() - 1);
}

int subSolution(vector<int>& nums, int l, int r) {
    if (l >= r) return 0;

    // Solve left and right parts
    int m = l + (r - l) / 2;
    int res = subSolution(nums, l, m) + subSolution(nums, m + 1, r);

    // Solve the left covers right part
    int i = l, j = r, p = m + 1;
    while(i <= m) {
        while(p <= r && nums[i] > (long)2 * nums[p])  p++;
        res += p - (m + 1);
        i++;
    }

    sort(nums.begin() + l, nums.begin() + r + 1);

    return res;
}

耗时长的原因是调用 sort，而别人调用 inplace_merge。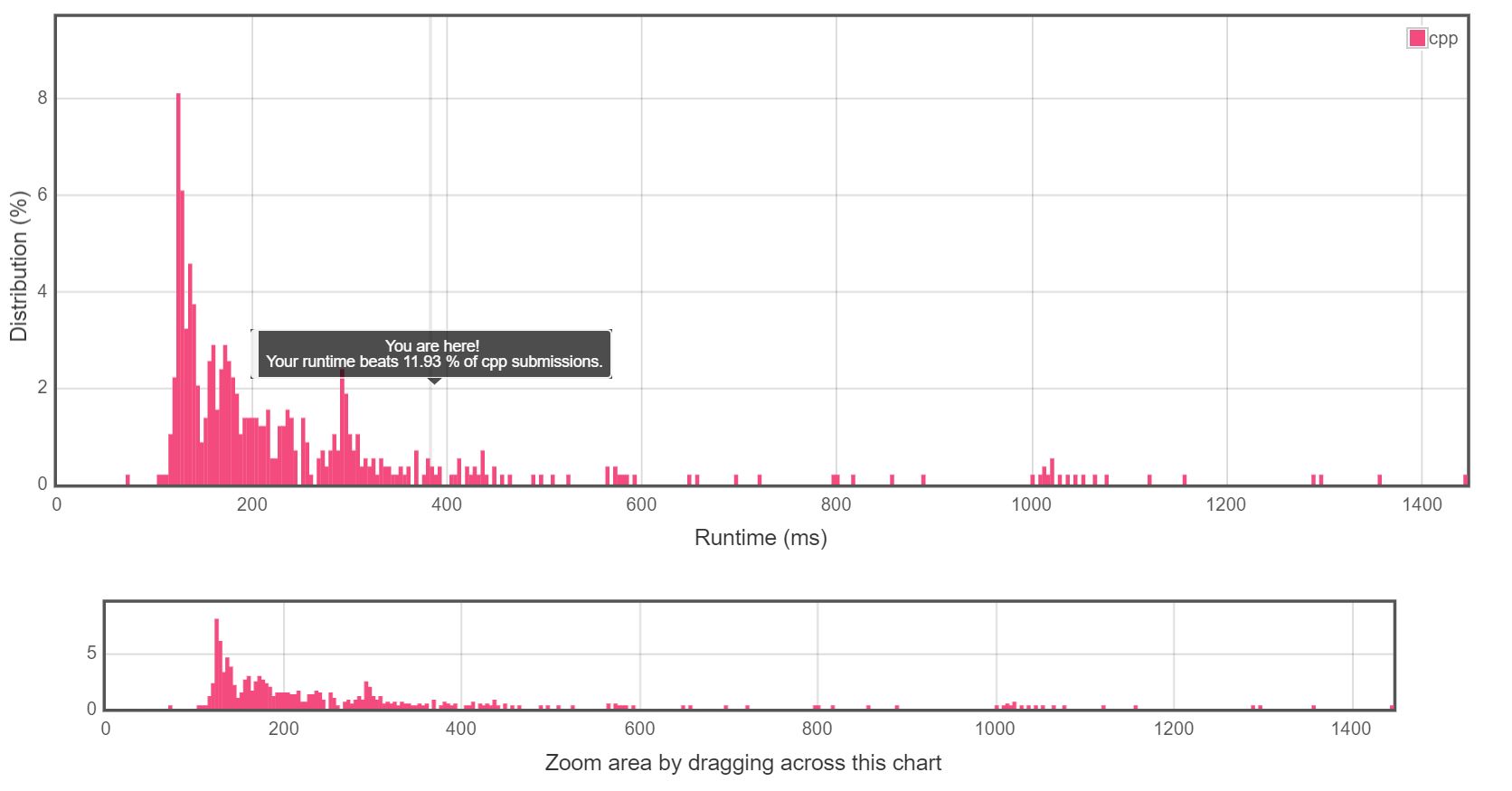
Time

Summary

这道题掌握的关于数组问题的分支想法，可以运用到其他数组题目上：Count Of Range Sum。

在这道题里，我们一样，划分子问题为 T(n) = 2T(n/2) + C，其中 C 为求解左右两数组内处于限制大小内的范围和个数。

Hint:
1. 定义累加和 s[i + 1] = s[i] + nums[i] 且 s[0] = 0
2. 那么范围和 [i, j] = s[j] - s[i - 1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int countRangeSum(vector<int>& nums, int lower, int upper) {
    int len = nums.size();
    vector<long> sum(len + 1, 0);
    for (int i = 0; i < len; ++i) {
        sum[i + 1] = sum[i] + nums[i];
    }
    return subSolution(sum, 0,  len + 1, lower, upper);
}

int subSolution(vector<long>& sum, int l, int r, int lower, int upper) {
    if (r - l <= 1) return 0;

    int m = l + (r - l) / 2;
    int res = subSolution(sum, l, m, lower, upper) +
        subSolution(sum, m, r, lower, upper);

    int p = m, q = m;
    for (int i = l; i < m; ++i) {
        while (p < r && sum[p] - sum[i] < lower) p++;
        while (q < r && sum[q] - sum[i] <= upper) q++;
        res += q - p;
    }

    auto itr = sum.begin();
    sort(itr + l, itr + r);

    return res;
}