Fork me on GitHub

Leetcode-Three-DFS

发表于 | 分类于 | 阅读次数:

Leetcode-Depth-First-Search

Path-Sum

Description

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.

Note: A leaf is a node with no children.

Example

Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

Analysis

这是一道标准的 DFS 题。我们直接对给出的二叉树，从根节点做一次 DFS，每查找一个节点，就算一次和，当在 叶结点 找到目标和则返回 true，就好了。

剪枝 是很容易想到的一个优化策略，当我们搜索到比目标和大的累加和时，可以不向下搜索。所以我一开始就写了剪枝，想着优化的 DFS 一定可以节省时间，结果…

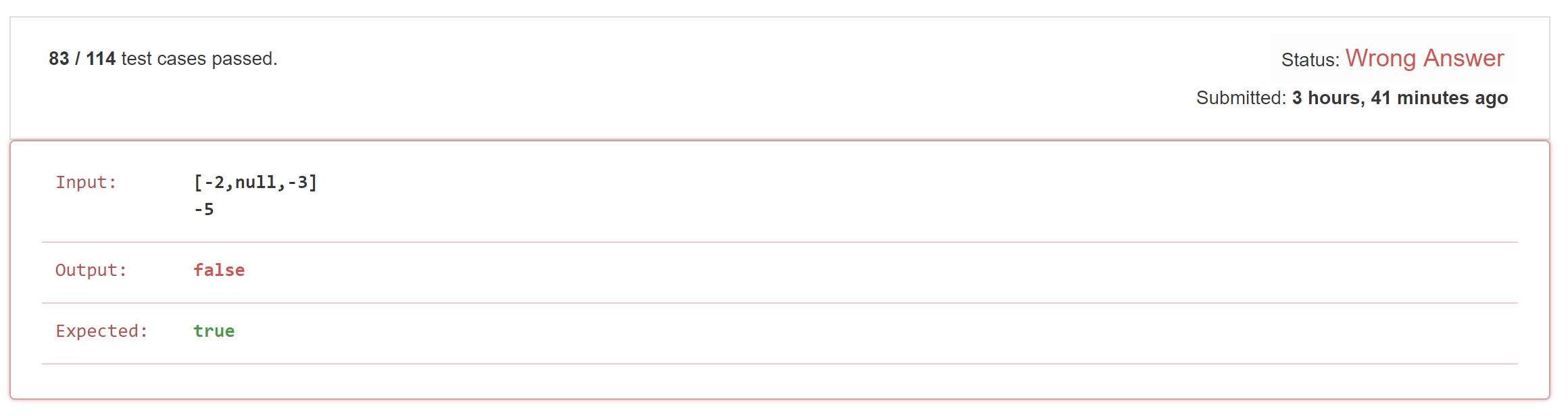
shortcut

输入是可以为负数的！样例只给了正数，但题目并没有说输入不能是负数。所以，剪枝是不可行的。用淳朴的 DFS 就好了。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        if (root == NULL)   return false;
        return dfs(root, 0, sum);
    }

    bool dfs(TreeNode* node, int sum, int target) {
        if (node == NULL)   return false;

        sum += node->val;
        if (sum == target && node->left == NULL && node->right == NULL)  return true;
        return dfs(node->left, sum, target) || dfs(node->right, sum, target);
    }
};

Sum-root-to-leaf-number

Description

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example

  • Example 1
    Input: [1,2,3]

      1
 / \
2   3

    Output: 25
    Explanation:
    The root-to-leaf path 1->2 represents the number 12.
    The root-to-leaf path 1->3 represents the number 13.
    Therefore, sum = 12 + 13 = 25.

  • Example 2:
    Input: [4,9,0,5,1] 

        4
   / \
  9   0
 / \
5   1

    Output: 1026
    Explanation:
    The root-to-leaf path 4->9->5 represents the number 495.
    The root-to-leaf path 4->9->1 represents the number 491.
    The root-to-leaf path 4->0 represents the number 40.
    Therefore, sum = 495 + 491 + 40 = 1026.

Analysis

对于给定一颗二叉树，计算一个根叶数字和。这个题目其实一样是 DFS，因为每一个加数，都是 DFS 到叶结点时的路径构成的。我们在 DFS 的时候，每遍历一个节点，将累加和乘以十，加上当前节点的值，到达叶结点时，将累加和作为加数，加入根叶数字和中，最后就得到结果。虽然是 medium 的题，但和前面的 easy 是一样的，只是 DFS 时的方法函数不一样。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int sumNumbers(TreeNode* root) {
        return dfs(root, 0, 0);
    }

    int dfs(TreeNode* node, int sum, int result) {
        if (node == NULL)   return result;

        sum = sum * 10 + node->val;
        if (node->left == NULL && node->right == NULL)
          return result + sum;

        return dfs(node->left, sum, result) +
          dfs(node->right, sum, result);
    }
};

BTree-Max-Path—Sum

Description

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example

  • Example 1
    Input: [1,2,3]

      1
 / \
2   3

    Output: 6

  • Example 2:
    Input: [-10,9,20,null,null,15,7]

     -10
 / \
9  20
  /  \
 15   7

    Output: 42

Analysis

题目求解的是二叉树中的任意路径的最大和，这个路径不需要经过根节点，只要是二叉树的一个包含节点的路径即可。与前面两道题目不一样，它的路径起点是不固定的了，这也是问题的难点。

我们抽象的来看这个问题：对于每一个节点，和它关联的最大路径和，必然由它的节点值和它的左右子树的最大路径和决定。我们通过求解节点的左子树和右子树的最大路径和，然后传递回上层，供节点值计算最大路径和，则可以计算出每一个节点与其相联子树能够达到的最大路径和。

采用这个指导思想，我们采用一个聪明的做法，from-bottom-to-top，利用 DFS，从底向上，一步一步计算每一层节点与其左右子树可以构成的最大路径和。然后直到最上层。每一次计算节点关联的最大路径和时，我们将这个最大路径和与全局变量 max 进行比较，那么就可以得到最终的最大路径和。

处理的细节：最大路径和为负数时，置为 0；空节点返回 0

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
static int desyncio = []() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);
    return 0;
}();

class Solution {
private:
    int max = INT_MIN;
public:
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return max;
    }

    int dfs(TreeNode* node) {
        if (node == NULL)   return 0;

        int l = dfs(node->left);
        if (l < 0)  l = 0;
        int r = dfs(node->right);
        if (r < 0)  r = 0;

        if (l + r + node->val > max)
          max = l + r + node->val;
        int temp = l > r ? l : r;
        return temp + node->val;
    }
};