ContainerWithMostWater

ContainerWithMostWater

Description

Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

Example

Input: [1,8,6,2,5,4,8,3,7]

Output: 49

Analysis & Code

题目大意是计算给定的柱子所能围成的最大面积。示例输出如图所示: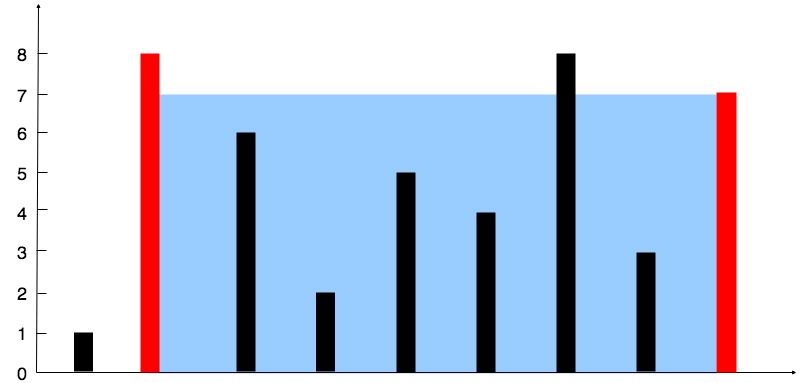
ContainerWithMostWater

首先明确一点，柱子之间的面积由 短板效应 决定，也就是最短的柱子决定了容器的高，而底为横坐标差的绝对值。

General Solution

然后很容易想到，可以利用 双重循环，对每一个柱子，扫描它后面的柱子，每次计算面积，然后更新最大面积。这样保证可以找到最大面积。
算法的时间复杂度是 $O(n^2)$ (实际上是 $\frac{n(n-1)}{2}$)
代码如下：

int maxArea(vector<int>& v) {
  int max = 0, temp = 0;
  for (int i = 0; i < v.size() - 1; ++i) {
    for (int j = i + 1; j < v.size(); ++j) {
      temp = (j - i) * (v[i] < v[j] ? v[i] : v[j]); 
      if (max < temp) {
        max = temp;
      }
    }
  }
  return max;
}

Advanced Solution

上面的算法时间复杂度为 $O(n^2)$，这是由双重循环导致的。可以考虑将循环缩减为一重，那么复杂度就下降到了 $O(n)$。下面来着手考虑如何优化算法。

我们可以发现一个事实，如果两根柱子确定的一个最大的”容量”，这个”容量”是针对较短的柱子而言。那么我们只要计算每一根柱子所能构成的最大”容量”，再比较出最大值，就可以得到所需的输出。

优化思路与证明如下：

假设当前两根柱子为最外侧的两个柱子，其围成的”容量”为V1。接下来，我们选择从某一侧向中间方向”移动”，选择一根新柱子，与另一侧的柱子构成新的”容器”，计算新的”容量”。
这里对于两侧的柱子有两种情况：
1. 柱子不等长
  
  如果从较长柱子侧向中间移动，那么对于较短柱子而言，新柱子无外乎三种情况：
  1. 比其短
    
    那么高和底都减小了，”容量”减小。
  2. 与其等长
    
    高不变，底变小，”容量”减小。
  3. 比其长
    
    高不变，底变小，”容量”减小。
    
    从该侧继续向中间移动，对于较短柱子而言，其”容量”都是不断减小的。所以，对于较短的柱子而言，最外侧的柱子是能与其构成最大容量的柱子。
2. 柱子等长
  
  那么无论从哪一侧开始移动，都是一样的，总有一根柱子的最大”容量”已经计算出来了。
我们采用递归的思维可以看出，从最外侧的两根柱子开始，每次选择一根新柱子，递归计算出每一根柱子对应的最大容量，那么答案就在这一次的遍历中。

代码如下：

int maxArea(vector<int>& v) {
  int maxArea = 0, temp = 0;
  int l = 0, r = v.size() - 1;
  while (l < r) {
    temp = (r - l) * (v[l] < v[r] ? v[l] : v[r]);
    if (maxArea <  temp) {
      maxArea = temp;
    }
    if (v[l] < v[r]) {
        l++;
    } else {
        r--;
    }
  }
  return maxArea;
}