Leetcode-Breadth-First-Search

Leetcode-Breadth-First-Search
- K-SimilarStrings
  - Description
  - Example
  - Analysis
  - Accept Picture
  - Code
  - Another Idea

K-SimilarStrings

Description

Strings A and B are K-similar (for some non-negative integer K) if we can swap the positions of two letters in A exactly K times so that the resulting string equals B.

Given two anagrams A and B, return the smallest K for which A and B are K-similar.

Note:

1 <= A.length == B.length <= 20
A and B contain only lowercase letters from the set {‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’}

Example

Example 1
Input: A = “ab”, B = “ba”
Output: 1
Example 2
Input: A = “abc”, B = “bca”
Output: 2
Example 3
Input: A = “abac”, B = “baca”
Output: 2
Example 4
Input: A = “aabc”, B = “abca”
Output: 2

Analysis

题目意思很明确：给出两个字符串 A，B。如果字符串 A 中的字符，经过交换 k 次，可以得到字符串 B，则称 A 与 B 为 K 相似串。现给出 A，B，求最小的 K。

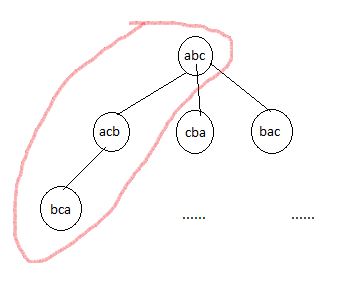
我们一步一步来分析。这是一个给定初始状态，计算到达目标状态的最短路径长度。查找最短路径的算法，我们用 BFS 算法。使用 BFS 算法，我们首先需要构造一张图。我们定义图的节点为字符串，节点的转换我们定义为字符串字符的swap(e.g.:节点 ab 通过交换 a 和 b 得到下一个节点 ba)。由此我们可以根据初始节点，通过 BFS 不停地生成(搜索)节点，查找达到目标节点的最短路径，也就是 K 值。我们举个 Example 例子来看看。

Example 2
Input: A = “abc”, B = “bca”
Output: 2

初始节点为 abc，可以经过 3 次不同的交换操作，生成(搜索)三个新节点，然后通过 BFS，可以在第二层搜索到目标节点，也得到最短路径2。

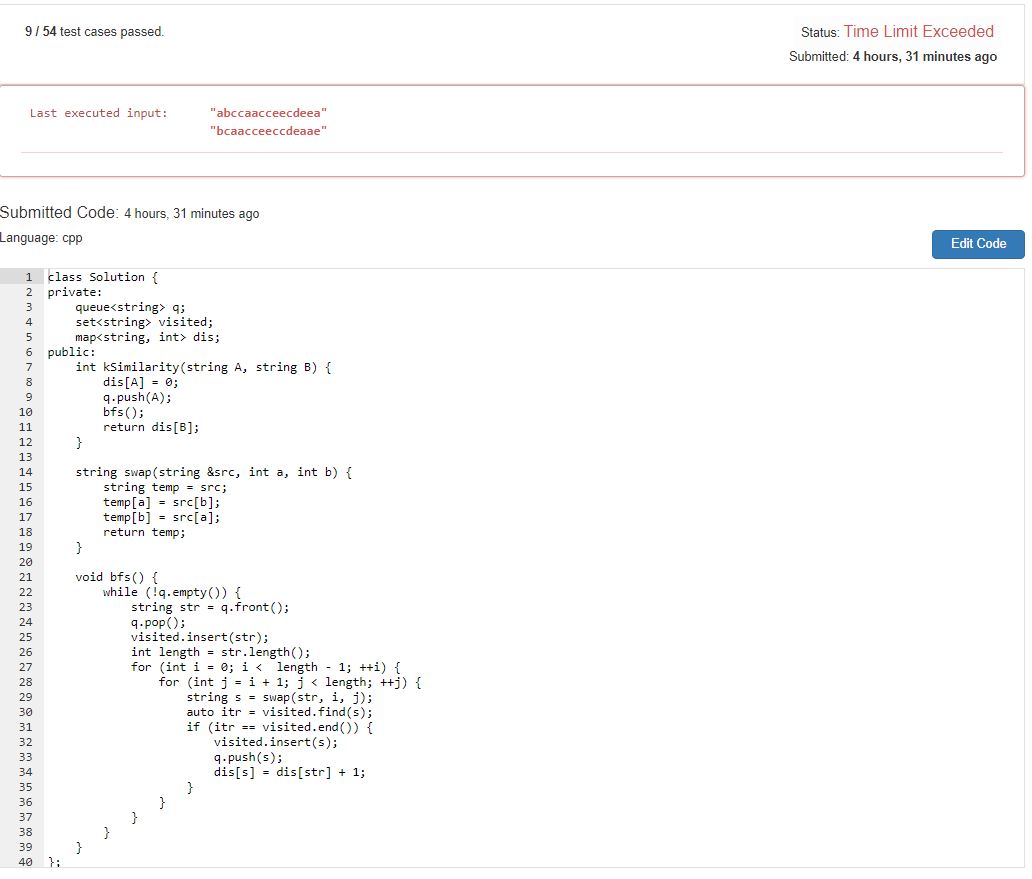
定义好了图的节点和节点转移方法，我们就可以写出第一版的 BFS了。我们来看看结果。大大的 TLE(23333)。

我们需要优化。我们在 BFS 中考虑了使用 visited 来标识访问过的节点，避免陷入死循环，实际上这对减少访问节点的个数，并没有太大的帮助。基础比较好的同学肯定知道，启发式搜索，这是可以帮助减少搜索节点个数，更快接近目标节点的进阶版 BFS。在这里，我们可以采取类似的思想，来减少搜索的节点个数。

我们可以模仿启发式搜索的思想来进行优化。我们对于当前搜索的节点，寻找其第一个与目标节点不匹配的字符，然后在这个字符后，寻找一个与目标节点匹配的字符进行交换，这样构造出来的节点，是我们继续搜索的节点。这样我们就大大减少了搜索的节点个数，因为交换后而没有向目标节点靠近的节点，会增加搜索层数，这必然不是在最短路径上的节点。这就是我们优化的核心思想。

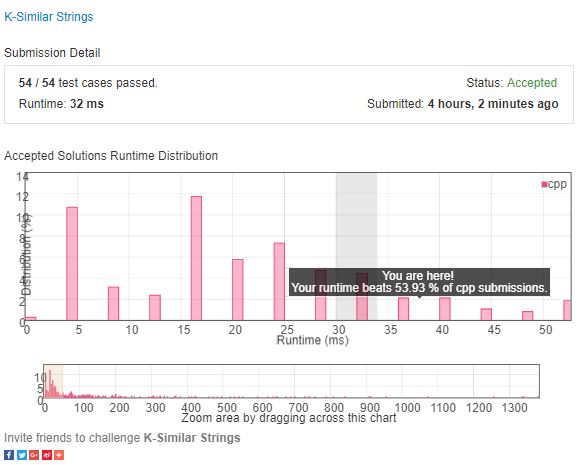
Accept Picture

前面梯队的速度差异，主要是 STL 库函数的使用，第一梯队使用的 DFS，是很神奇的做法。
Accept

Code

static int desyncio = []() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);
    return 0;
}();

class Solution {
private:
    queue<pair<string, int> > q;
    set<string> visited;

    int length;
public:
    int kSimilarity(string A, string B) {
        if (A == B) return 0;

        length = A.length();

        int i = 0;
        while (i < length) {
            if (A[i] != B[i])   break;
            ++i;
        }
        q.push({A, i});
        visited.insert(A);

        return bfs(B, 0);
    }

    int bfs(string &target, int step) {
        while (!q.empty()) {
            int size = q.size();
            for (int i = 0; i < size; ++i) {
                string str = q.front().first;
                int index = q.front().second;
                q.pop();

                if (target == str)  return step;

                while (str[index] == target[index])	++index;

                for (int n = index + 1; n < length; ++n) {
                if (str[n] != target[n] && str[n] == target[index]) {
                        swap(str[index], str[n]);
                        auto itr = visited.find(str);
                        if (itr == visited.end()) {
                            visited.insert(str);
                            q.push({str, index + 1});
                        }
                        swap(str[index], str[n]);
                    }
                }
            }
            ++step;
        }
        return step;
    }
};

Another Idea

前面使用的优化是直接减少搜索的节点个数，我们还是可以利用启发式搜索的思路的。A*是常用的一种启发式搜索，主要是其中的代价函数，我们可以仿照代价函数，使用优先队列来对搜索节点进行排序，其中，定义正确字符个数越多的节点，优先级越高。这样也可以加快搜索的速度。

这只是一个想法，感知可行，至于真实性，留待考验。