CFL-Problem

Capacitated Facilities Location Problem - the project for Algorithm Course.

Description

Suppose there are $n$ facilities and $m$ customers. We wish to choose:

which of the $n$ facilities to open
the assignment of customers to facilities

The objective is to minimize the sum of the opening cost and the assignment cost.

The total demand assigned to a facility must not exceed its capacity.

There are currently 71 data files.

Data File Format

$J,I$
$s_1,f_1$
$s_2,f_2$
$…$
$s_J,f_J$
$d_1,d_2,d_3,…,d_I$
$c_{11},c_{12},c_{13},…,c_{1I}$
$c_{21},c_{22},c_{23},…,c_{2I}$
$…$
$c_{J1},c_{J2},c_{J3},…,c_{JI}$

where:

$J$ is the number of potential facility locations;
$I$ is the number of customers;
$s_j (j=1,…,J)$ is the capacity of facility $j$;
$f_j (j=1,…,J)$ is the fixed cost of opening facility $j$;
$d_i (i=1,…,I)$ is the demand of customer $i$;
$c_{ji} (j=1,…,J), (i=1,…,I)$ is the cost of allocating all the demand of customer $i$ to facility $j$.

Analysis

题目的意思很明显，每一个算例，有 $J$ 个工厂， $m$ 个顾客。每个工厂有固定的开设成本，服务不同顾客的不同服务成本和容量；每个顾客有需求。现在要决定怎么分配服务顾客的工厂，使得工厂服务的顾客的总需求不会超出其容量，同时所有工厂的总成本最小。

这是一个搜索问题，如何在解空间内找到一个最优解，即在所有的合法分配方案中，找到一个成本最小的方案。

这里我使用一个局部搜索算法和一个启发式搜索算法来解决这个问题。一个显然的事实是，无论局部搜索还是启发式搜索，两者生成的解空间必定是问题整体解空间的子集，所以找到的最优解都不一定是真正的最优解，但是是自己搜索的解空间中的最优解。

但使用这样的搜索算法，可以在有限的时间里得到一个较好的方案，而不用耗费大量时间，穷举搜索完整的解空间。

Algorithm Design

如前文所述，这里采用一个局部搜索算法和一个启发式搜索算法。我的选择是贪心的爬山算法(Hill Climbing Algorithm)和遗传算法(Genetic Algorithm)。

两个算法都不是很难，建议先了解，具体流程不在此介绍

为何说爬山算法是贪婪的呢？因为在每一次的邻域选择时，它选择的是最优的那个解。但是这样的选择策略是没办法保证一定能找到最优解的，因为最优解可能是通过其他较次解得到的。所以爬山算法的缺点也很明显，找到的解可能是局部最优解。

至于遗传算法，它模仿自然界中的种群繁衍过程。每一次迭代在种群中选择出存活个体，存活个体间进行交叉变异，生成下一代并和存活个体共同构成下一个种群。

大概过程如图：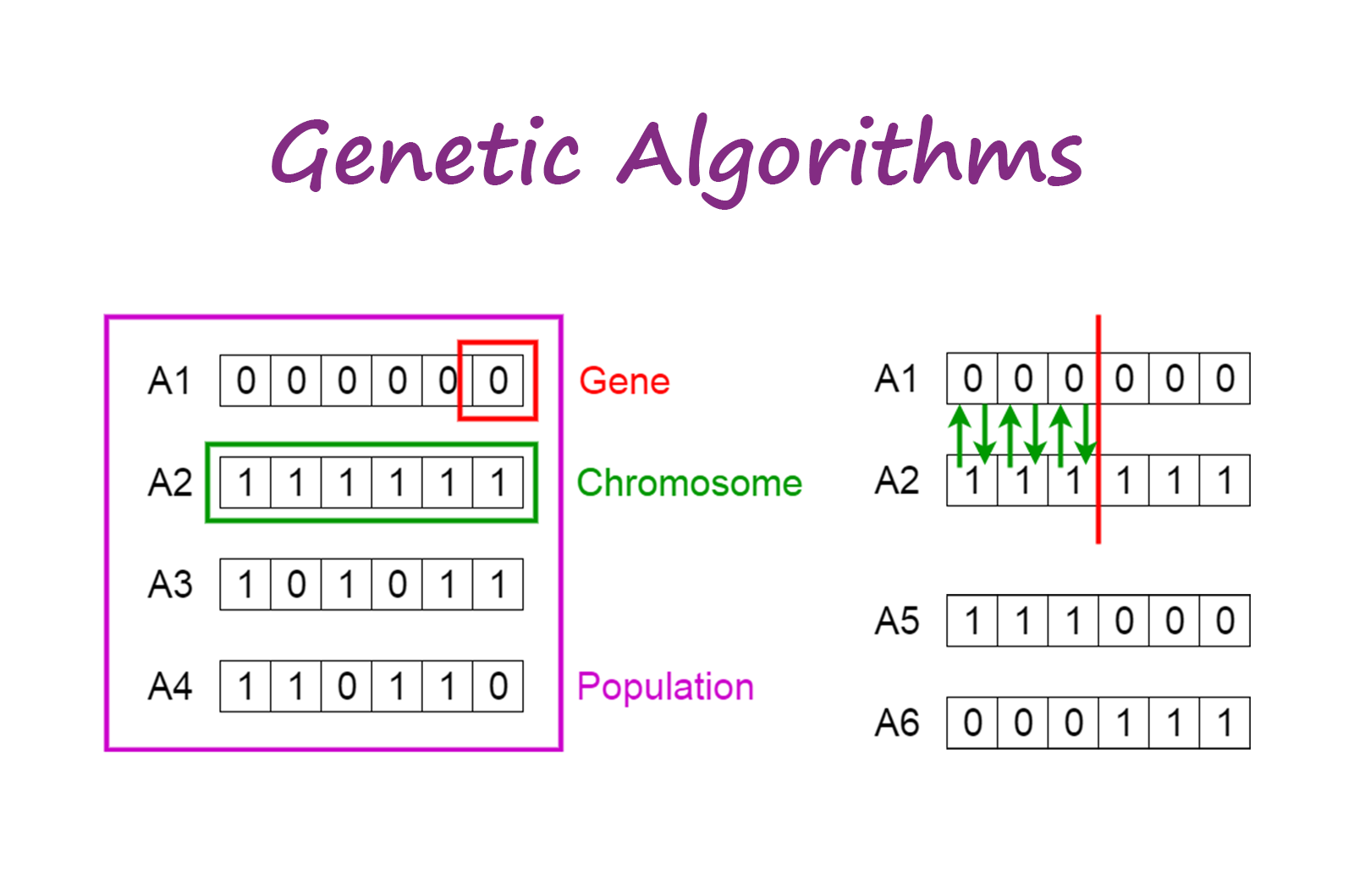

这里先介绍一下对于解的定义。题目的关键是分配工厂给顾客，所以我们将解定义为一个数组，数组长度为顾客数量，数组元素为每一个顾客分配的工厂。这样的解，对于各种操作都是十分方便的：

合法性

遍历数组，统计每个工厂分配的总顾客需求，如果超出容量则非法
工厂开关状态

遍历数组，对于分配了顾客的工厂，设为打开即可
解的总成本

得到工厂开关状态后，叠加开设成本；遍历数组，叠加分配成本
生成新解

修改数组元素，就是一个新解

定义好了解，下面介绍两个算法的设计。

Hill Climbing Algorithm

爬山算法从当前解，根据邻域操作，生成一个邻域空间(局部解空间)，然后从邻域空间内找到一个最优解。对比当前解和找到的最优解，如果找到的解比当前解更优，那么就替换当前解。重复算法，直到找不到更优的解，则结束算法。伪代码如下：

Solution curNode, nextNode
Neighborhood n = generate(curNode)
nextNode = bestSolution(n)
while curNode.cost > nextNode.cost:
    curNode = nextNode
    n = generate(curNode)
    nextNode = bestSolution(n)

算法中的 cost 就是我们的分配方案成本，bestSolution(n) 就是在邻域 n 中查找拥有最低成本的分配方案。需要设计的就是如何生成一个邻域，也就是 generate(curNode)。

邻域空间的生成需要设计邻域操作，也就是对当前解进行某种操作，生成一个新的解，这个解就属于我们生成的邻域。所以，我们需要设计的就是邻域操作。这里我设计了4个邻域操作：

随机交换两个顾客的分配工厂
将三个连续顾客的分配工厂重排序(e.g: a, b, c-> b, c, a)
对当前分配方案随机排序
逆序当前分配方案

对于当前解，前3个邻域每个执行操作5000次，最后一个执行一次，这样邻域空间大小就达到了 15001，然后从中找出一个最优解。

Genetic Algorithm

遗传算法，每一次迭代在当前解空间中选择出部分解，解之间进行交叉变异操作生成新解，这些新解和选择出的解共同构成下一个解空间。伪代码如下：

Solution s
Population curP, selection, generation
while True: # Loop until iteration times is satisfied
    selection = select(curP)
    for solution in selection:
        s = crossOver(solution)
        s = mutation(s)
        generation.add(s)
    curP = selection + generation

这里可以运用 GA 也得益于解的定义。因为对于解可以表示成数组的搜索问题，是可以使用 GA 的。因为数组可以看作一个染色体，数组元素就是基因，这样染色体的交叉变异操作就可以看作数组元素的操作。
在这里，需要设计的函数是 select(curP)，crossOver(solution), mutation(s)，也就是选择，交叉(遗传)和变异操作。

选择

选择就如同自然选择，不过我们是上帝，操纵着选择过程。这里我使用 $k=2$ 的竞标赛(Tournament Selection)的方法来选择个体。也就是说，随机从种群中挑选两个个体，优胜劣汰。这样选择出来的个体总数为种群数的一半(这里选择淘汰的个体没有再次被选择的机会，也就是无重复)。
交叉(遗传)

交叉(遗传)模仿自然界个体交配过程中的染色体行为：父母双方染色体的一半重新结合，生成新个体。这里的交叉过程，有多种方法：单点交叉，两点交叉，均匀交叉等(尝试过三种交叉，最终选择了两点交叉，不过更公平且符合求解逻辑的是均匀交叉)。
这里选择两点交叉，也就是在解中随机选择两个位置，交换两个亲代位置区段的数组元素，生成两个新的解。
变异

变异和自然界的基因变异是类似的。基因是可以突变的，所以在交叉完毕后，对于每一个子代，应该进行一次变异操作(基于变异概率)。
变异的方法和交叉一样，有多种方法。这里我选择的是整体变异，也就是对于解数组中的每一个元素，遍历变异。变异就是替换为一个随机元素。

Architecture

├── Instance.hpp    // Initialize an instance from instance file and contains the info inside the instance file
├── Solution.hpp    // Initialize an instance of solution which contains the allocation of customers
├── HC.hpp  // Initialize an instance of Hill Climbing Algorithm which could be performed on an instance
├── GA.hpp  // Initialize an instance of Genetic Algorithm which could be performed on an instance
└── main.cpp    // Program entry

Instance.hpp

class Instance {
public:
    int facility_num;   // facility number
    int customer_num;   // customer number
    vector<int> capicity; // capicity of facilities
    vector<int> open_cost;   // open cost of facilities
    vector<int> demand; // demand of customers
    vector<vector<int> > allocate_cost; // allocate cost of facilities

    Instance(string filePath);
};

Solution.hpp

class Solution {
public:
    vector<int> allocate; // Allocation of all customers
    vector<int> serving; // Serving customer count for each facility

    Solution();
    Solution(int &facilityNum, int &customerNum);
    Solution(vector<int> &v, int facilityNum);
    bool isValid(vector<int> &capicity, vector<int> &demand);
    vector<int> getFacilityState();
    int getCost(vector<int> &open, vector<vector<int> > &allocation, vector<int> &capicity, vector<int> &demand);
    bool operator == (const Solution &p2) const;
};

HC.hpp

class HC {
public:
    Solution twoOpt(Solution &s);   // Swap two allocations between two random chosen customer
    Solution threeOpt(Solution &s); // Reorder the allocations among three continuous customers(e.g: a, b, c-> b, c, a)
    Solution randomOpt(Solution &s);    // Randomly rearrange the allocations with the current allocations
    Solution reverseOpt(Solution &s);   // Reverse the allocations
    vector<Solution> neighborHood(Solution &s); // Generate the neighborhood
    Solution nextSolution(Solution &s, vector<int> &open, vector<vector<int> > &allocation,
        vector<int> &capicity, vector<int> &demand);    // Find the best solution in neighborhood
};

GA.hpp

class GeneAlgorithm {
public:
    int crossRate;  // CrossOver rate
    int mutationRate;   // Mutation Rate
    vector<Solution> population;    // Population
    vector<Solution> selection; // Selection of population
    vector<Solution> generation;    // Generation of Selection

    GeneAlgorithm(int size, int crossRate, int mutationRate, int &facilityNum, int &customerNum, vector<int> &capicity, vector<int> &demand);
    void Selection(vector<int> &open, vector<vector<int> > &allocate, vector<int> &capicity, vector<int> &demand);
    void CrossAndMutate(vector<int> &capicity, vector<int> &open, vector<vector<int> > &allocate, vector<int> &demand);
    vector<int>& Mutation(vector<int> &g);
    Solution bestSolution(vector<int> &open, vector<vector<int> > &allocate, vector<int> &capicity, vector<int> &demand);
};

main.cpp

void performGA(Instance &instance, int index, FILE* result, int ga_size, int ga_crossRate, int ga_mutationRate);
void performHC(Instance &instance, int index, FILE* result);

int main() {
    int ga_size, ga_crossRate, ga_mutationRate;

    cout << "GA: Population Size, CrossOver Rate, Mutation Rate: " << endl;
    cin >> ga_size >> ga_crossRate >> ga_mutationRate;

    FILE* resultGA = fopen("resultGA.csv", "w");
    FILE* resultHC = fopen("resultHC.csv", "w");
    if (resultGA == nullptr) {
        cout << "Fail to open file: resultGA.csv" << endl;
        return 0;
    }
    if (resultHC == nullptr) {
        cout << "Fail to open file: resultHC.csv" << endl;
        return 0;
    }
    fprintf(resultGA, "%s\n", "Instance,Time,Cost,FacilityState,CustomerState");
    fprintf(resultHC, "%s\n", "Instance,Time,Cost,FacilityState,CustomerState");	

    string filePath;
    for (int i = 1; i <= 71; ++i) {
        cout << "START Read File..." << endl;
        string instancePath = "../Instance/p" + std::to_string(i);
        Instance instance(instancePath);
        performHC(instance, i, resultHC);
        performGA(instance, i, resultGA, ga_size, ga_crossRate, ga_mutationRate);
    }

    fclose(resultGA);
    fclose(resultHC);
}

Code

完整代码见Github
内带代码调用注释

Comparison

下面来比较一下两个算法的结果。完整结果见Github，这里列举每个算法的前三个和最后三个算例的结果。

可以很明显的看出，在较为简单的算例(前3个)，GA 和 HC 的运行时间相近，但是 GA 得到的结果比 HC 要好得多，这也能验证 HC 的缺点，很难跳出局部最优解。

但是在后面较为复杂的例子(可以比对算例33-37)，HC 的运算速度较 GA 快，但是结果却十分的差，GA 运行时间几乎是 HC 的3 倍，但是解的优化是 HC 的两倍。

表格更明显的一个地方：工厂的开关状态，对于 HC 来说，它的选择基本是开设全部工厂，然后调整分配成本，来达到最优，这又是局部的一种体现，它并没有考察到开设成本。而对于 GA 来说，它开设工厂是有选择的。

Result for Genetic Algorithm

Instance	Time(s)	Cost	FacilityState	CustomerState
1	4	9272	1 0 1 1 1 1 1 0 1 1	9 3 6 7 4 9 3 5 5 6 10 1 4 3 9 4 5 1 10 5 4 3 7 5 3 6 4 6 1 6 3 7 1 1 10 5 5 4 1 5 6 9 4 6 5 1 5 1 5 4
2	3	8063	1 1 1 1 1 1 0 0 1 1	9 3 2 6 4 9 3 5 5 2 10 1 4 3 9 4 5 1 10 5 4 3 10 5 3 6 2 6 1 6 3 6 1 4 10 5 5 4 1 5 2 9 2 6 5 1 5 1 5 1
3	3	9788	1 1 1 1 1 1 1 0 1 1	9 3 2 7 4 9 3 5 5 2 10 9 4 3 1 4 3 1 10 5 4 5 7 5 3 6 2 6 1 6 3 7 1 4 10 5 5 4 1 5 2 9 2 6 5 1 5 1 5 1
…	…	…	…	…
69	56	43845	1 1 1 0 0 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1	19 7 28 1 22 13 22 18 25 28 27 29 15 2 29 8 2 18 19 28 18 28 6 25 18 13 28 18 30 17 27 20 27 17 28 13 21 9 25 22 23 11 13 10 9 20 9 22 15 29 25 17 3 17 21 13 19 10 23 8 20 25 8 15 10 12 2 11 20 13 19 7 27 21 11 11 11 1 9 17 11 3 10 26 7 11 7 25 23 26 12 12 12 12 3 2 12 7 1 29 20 17 13 19 30 18 7 17 19 2 18 30 26 26 13 9 29 8 19 21 15 12 29 13 10 23 22 13 15 10 19 3 8 9 21 27 2 11 1 2 13 22 7 26 13 25 25 17 19 26 25 18 18 1 9 12 6 17 11 9 2 26 6 25 3 29 6 30 9 22 2 21 27 21 27 3 22 30 27 21 6 3 22 15 29 11 7 6 18 22 25 25 20 7 8 20 19 1 18 20
70	83	59837	1 1 1 0 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 0	12 12 6 28 3 15 22 28 26 13 27 18 11 24 12 12 2 11 19 20 28 17 3 25 24 19 1 27 27 16 20 27 27 17 28 13 24 21 25 17 19 9 13 27 21 20 14 25 20 21 1 3 17 25 15 7 25 27 28 12 27 1 19 9 24 26 3 15 26 12 1 13 15 21 24 11 2 3 21 17 11 3 9 26 27 14 7 18 25 19 25 27 20 12 28 2 13 20 18 19 18 16 26 26 7 3 20 25 28 21 14 20 28 13 7 21 20 26 18 9 15 12 18 20 9 17 3 13 20 1 13 19 26 20 2 9 9 14 18 9 12 22 13 26 12 6 3 16 19 26 25 11 14 11 2 19 22 16 14 14 21 25 3 24 1 28 24 20 2 17 14 14 20 21 27 3 3 21 20 24 6 16 17 20 13 27 18 11 11 25 17 3 13 7 13 12 19 22 11 7
71	37	50943	1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1	19 20 22 12 1 18 16 29 1 29 30 18 11 14 15 19 24 15 22 25 12 25 25 28 15 19 19 29 30 3 20 7 7 17 19 7 15 4 1 17 19 10 20 18 9 7 4 22 29 10 28 25 3 22 9 13 19 10 19 28 27 1 28 14 4 8 22 27 29 12 8 7 11 30 11 10 4 24 24 28 24 11 27 26 30 15 5 1 3 8 12 7 13 26 11 14 29 12 18 29 18 22 26 8 5 1 5 3 17 14 20 5 25 7 13 4 28 8 1 11 4 26 3 20 10 25 1 12 15 18 29 22 13 18 6 9 14 15 29 3 13 28 15 12 26 6 19 16 22 26 28 18 22 1 11 20 22 22 4 24 4 18 11 3 6 29 6 27 4 3 6 9 20 15 27 6 28 15 30 11 24 22 22 24 13 9 29 9 3 22 3 22 15 19 8 12 26 3 3 7

Result for Hill Climbing Algorithm

Instance	Time(s)	Cost	FacilityState	CustomerState
1	3	10854	1 1 1 1 1 1 1 1 1 1	9 3 6 7 4 9 3 10 10 6 10 1 4 3 9 4 10 1 7 8 4 8 7 10 6 6 2 6 1 6 7 7 1 3 10 5 5 4 1 10 6 9 2 6 8 1 10 1 5 4
2	3	9218	1 1 1 1 1 1 1 1 1 1	8 3 2 7 2 9 3 10 8 2 10 9 4 3 9 4 3 1 7 8 6 8 7 5 6 6 2 6 1 6 7 7 1 3 10 5 5 4 1 10 6 9 2 7 8 1 10 1 8 1
3	4	10777	1 1 1 1 1 1 1 1 1 1	8 3 2 7 2 9 3 5 5 6 10 9 4 3 9 4 5 1 10 8 6 8 7 5 6 6 2 6 1 6 7 7 1 4 10 5 5 4 1 5 6 9 2 6 8 1 10 4 5 4
69	47	35788	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	19 20 22 23 3 13 16 28 23 29 5 15 14 2 20 19 2 11 23 28 19 17 6 25 11 19 28 15 30 3 20 5 5 17 28 7 21 9 28 16 19 10 7 30 4 27 4 22 20 15 28 23 22 17 21 7 12 10 19 8 30 1 8 21 14 12 24 15 20 26 19 13 7 10 24 24 14 24 14 23 11 1 10 8 30 14 5 3 28 8 29 7 8 26 3 4 28 7 1 29 15 16 13 19 5 1 30 28 23 4 20 30 28 13 13 9 29 8 11 9 10 12 18 20 27 23 3 7 27 18 12 22 12 11 14 10 2 4 29 11 13 23 7 26 26 6 25 16 28 26 28 18 24 1 4 12 3 16 4 4 14 28 11 3 6 28 6 30 2 22 2 21 20 15 27 3 1 11 30 11 3 22 22 20 13 9 20 24 1 22 3 22 7 5 8 13 8 16 11 22
…	…	…	…	…
70	49	59980	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	19 20 22 28 6 30 16 18 23 18 30 15 14 2 15 19 2 21 23 18 19 17 2 25 11 28 28 15 30 2 27 27 5 17 28 5 21 9 25 22 19 10 7 30 21 27 14 22 27 15 1 22 3 22 21 7 29 10 19 12 30 1 8 21 14 12 24 15 15 26 8 13 27 10 24 24 21 2 21 23 14 11 10 26 30 14 5 6 28 8 29 5 12 26 24 2 29 7 11 29 15 16 13 19 5 1 30 25 23 4 27 30 28 7 7 9 29 12 15 21 27 12 18 27 27 17 3 29 27 18 29 25 13 21 2 10 2 4 15 15 13 23 20 12 26 6 25 16 28 26 1 18 24 18 14 29 6 16 4 14 14 18 11 3 24 28 2 30 2 22 2 21 15 15 27 3 1 21 30 11 2 22 3 20 7 9 29 14 1 22 3 22 5 30 8 5 8 2 11 27
71	47	41641	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	19 20 22 23 3 13 16 28 23 18 5 18 24 2 20 19 2 21 23 1 28 17 6 25 24 19 23 15 30 22 20 27 5 17 28 5 21 9 25 16 8 10 7 27 9 27 14 22 20 15 25 17 25 22 9 7 12 10 23 8 5 1 8 9 14 12 6 15 20 12 8 13 20 10 6 24 21 6 9 25 24 18 10 26 5 14 5 3 28 8 18 20 12 12 3 2 29 7 1 29 18 16 12 8 5 1 5 25 23 4 15 5 28 7 13 9 29 8 18 9 27 12 18 27 27 17 22 12 27 18 29 25 12 24 2 10 2 4 18 15 13 23 7 12 26 3 25 16 28 26 25 18 24 1 9 29 3 16 4 14 2 28 24 25 6 28 6 5 2 22 2 21 15 15 27 3 1 15 30 11 6 16 25 20 13 10 29 24 1 22 3 22 7 5 8 13 8 16 11 5